Quantum Intelligent Agents discover cornerstone quantum algorithms

Quantum computing offers a fundamentally different approach to computation compared to classical computers that has led to the development of groundbreaking quantum algorithms and cryptographic protocols. Despite these advancements, challenges remain in discovering practical quantum applications due to the complexities of quantum information and the limitations of current hardware. Concurrently, Artificial Intelligence (AI) has revolutionized computation through self-learning systems like neural networks and reinforcement learning, exemplified by DeepMind’s AlphaGo and AlphaFold, or OpenAI's ChatGPT. Quantum Intelligence aims to combine quantum technologies with AI and envisions agents enhanced with quantum capabilities to optimize their actions and solve complex problems. 

In our recent manuscript, we take a further step forward towards the goal of quantum intelligence by demonstrating how quantum intelligent agents can discover a number of quantum algorithms and interactive quantum protocols/games that have been a cornerstone of quantum information. First, we show how such a quantum agent can learn how to perform the Quantum Fourier Transform optimally, namely with a logarithmic size, nearest-neighbor connectivity circuit. Then, we show how they can discover Grover's algorithm for search. In addition, we show how quantum intelligent agents can self-learn to optimally win the CHSH game, and find the optimal cheating strategies in coin flipping protocols. Our work opens the way to what we believe is a novel paradigm for finding quantum protocols and algorithms via quantum intelligence. We expect that these techniques can be pushed much further to the development of novel quantum algorithms. 

More details about how we trained our quantum intelligent agents can be found in the manuscript {} and all experiments and code are available at https://github.com/Quantum-Signals/self-play-quantum

The example of the Quantum Fourier Transform

The Quantum Fourier Transform is one of the seminal quantum algorithms that performs the discrete Fourier Transform on an n-dimensional  vector encoded as a quantum state of logn qubits, with a quantum circuit of size polylog(n). This is one of the few exponential quantum advantages, since the discrete Fourier Transform takes time linear in n and it is an essential part of the quantum factoring algorithm and of quantum phase estimation.

Our goal is to find a quantum circuit for performing the Quantum Fourier Transform that has logarithmic size and uses nearest-qubit connectivity, as our quantum intelligent agents. 

We start by trying to find the QFT circuit for input size n=16 (i.e. 4 qubits) and n=64 (i.e. 6 qubits). The quantum intelligent agent trained to perform the QFT for these input sizes, so then we started simplifying the agent to see how much simpler of a circuit we can get. In the end, we ended up with a very simple quantum circuit with optimal parameters. 

The reward of the quantum agent is calculated by averaging over a batch of inputs the l2 distance between the actual Fourier Transform versus the output of the quantum agent. One can find the details of the training in the paper, including the choice of optimizer, learning rate, initialization etc. 

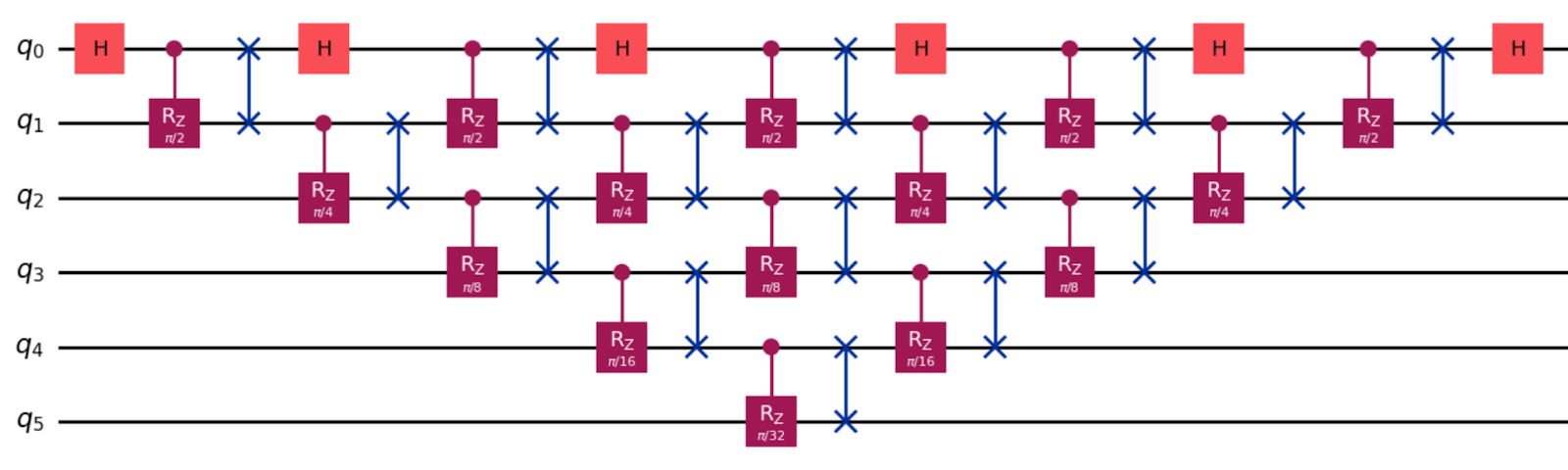
The training for n=16 after 300 epochs provided a reward of  0.9999999999990983 and in Fig.1 we can see the trained quantum agent. Note that all gates with parameters 0 can be removed, since they apply the Identity matrix. The structure of the circuit is very clear. The single qubit gates on the first qubit of the pyramid are Hadamard gates (up to phases), while the matchgates perform a SWAP operation between the qubits and add a phase that cascades through the pyramid between values very close to π/2, π/4, π/8.. 

We redid the training for n=64. Again, the best score was 0.9999999860160202 and the trained circuit as in Fig.2. The exact same structure appears. Hadamard gates (up to phases) on the first qubit, and matchgates that perform cascading phase gates and swap operations between the qubits. 

Given these results it is extremely straightforward for a human with basic knowledge of quantum to provide the general QFT algorithm for any input n. We show in Fig.3 the case of n=64, i.e. 6 qubits. Note that is not exactly the same QFT algorithm one finds in the textbooks or Wikipedia, because our quantum agent needed to respect the nearest-qubit connectivity, but it is the optimal circuit for such architectures, with logn qubits, 2logn depth, logn(logn -1) 2-qubit gates (SWAP and CRZ gates), and logn single-qubit gates. 

What is next?

We are strong believers in the synergy of quantum and AI. Our quantum intelligent agents are a powerful example of the potential of quantum intelligence and we are seeing just the beginning. Here are some of our ideas for the future.

Novel quantum algorithms

Our next goal is to use our quantum intelligent agents within supervised and reinforcement learning frameworks to discover novel quantum algorithms. .We think it is totally possible and we are working on it on our side. By sharing this write-up and making the code open source we encourage researchers to try themselves as well. Some obvious questions can include looking for other transforms, such as generalizations of the Fourier Transform, better error correcting circuits, novel cryptographic primitives, etc. One can also use our quantum intelligent agents to play classical or quantum games, or use them as a way to benchmark quantum hardware by letting them play against each other.     

Quantum Intelligent Agents for Finance

In the future, we are planning to incorporate quantum intelligent agents to provide state-of-the-art trading strategies. Such quantum agents are trained in an exponentially large Hilbert state and can provide interesting models that can be used by themselves or in ensemble methods together with classical ones. While the quantum hardware is getting ready for primetime we are working tirelessly to understand the best way to use such quantum agents to bring intelligent trading to the future.

Stay tuned to our progress by signing up for updates.